paper

Community Detection(1)

Posted by Firef1y on April 9, 2020

We propose a new nonlinear factorization model for graphs that are with topological structures, and optionally, node attributes. This model is based on a pseudometric called Gromov-Wasserstein (GW) discrepancy, which compares graphs in a relational way. It estimates observed graphs as GW barycenters constructed by a set of atoms with different weights. By minimizing the GW discrepancy between each observed graph and its GW barycenter-based estimation, we learn the atoms and their weights associated with the observed graphs. The model achieves a novel and flexible factorization mechanism under GW discrepancy, in which both the observed graphs and the learnable atoms can be unaligned and with different sizes. We design an effective approximate algorithm for learning this Gromov-Wasserstein factorization (GWF) model, unrolling loopy computations as stacked modules and computing gradients with backpropagation. The stacked modules can be with two different architectures, which correspond to the proximal point algorithm (PPA) and Bregman alternating direction method of multipliers (BADMM), respectively. Experiments show that our model obtains encouraging results on clustering graphs.

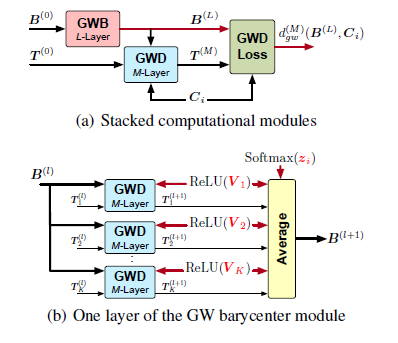
image

基于分解的learning 方法很高级，不强调结构和属性

  • 2.Discrete Optimal Graph Clustering (IEEE Cybernetics 2019 一区)

Graph based clustering is one of the major clustering methods. Most of it work in three separate steps: similarity graph construction, clustering label relaxing and label discretization with k-means. Such common practice has three disadvantages: 1) the predefined similarity graph is often fixed and may not be optimal for the subsequent clustering. 2) the relaxing process of cluster labels may cause significant information loss. 3) label discretization may deviate from the real clustering result since k-means is sensitive to the initialization of cluster centroids. To tackle these problems, in this paper, we propose an effective discrete optimal graph clustering (DOGC) framework. A structured similarity graph that is theoretically optimal for clustering performance is adaptively learned with a guidance of reasonable rank constraint. Besides, to avoid the information loss, we explicitly enforce a discrete transformation on the intermediate continuous label, which derives a tractable optimization problem with discrete solution. Further, to compensate the unreliability of the learned labels and enhance the clustering accuracy, we design an adaptive robust module that learns prediction function for the unseen data based on the learned discrete cluster labels. Finally, an iterative optimization strategy guaranteed with convergence is developed to directly solve the clustering results. Extensive experiments conducted on both real and synthetic datasets demonstrate the superiority of our proposed methods compared with several state-of-the-art clustering approaches.

image

提出初步的formulation

为了解决实际问题优化算法

确定参数值

复杂性分析

聚合性分析

a discriminaltive subspace for data clustering

projective subspace learning

有一个贼高级的方法

  • 3.vGraph: A Generative Model for Joint Community Detection and Node Representation Learning (NeurIPS 2019 A类)

This paper focuses on two fundamental tasks of graph analysis: community detection and node representation learning, which capture the global and local structures of graphs, respectively. In the current literature, these two tasks are usually independently studied while they are actually highly correlated. We propose a probabilistic generative model called vGraph to learn community membership and node representation collaboratively. Specifically, we assume that each node can be represented as a mixture of communities, and each community is defined as a multinomial distribution over nodes. Both the mixing coefficients and the community distribution are parameterized by the low-dimensional representations of the nodes and communities. We designed an effective variational inference algorithm which regularizes the community membership of neighboring nodes to be similar in the latent space. Experimental results on multiple real-world graphs show that vGraph is very effective in both community detection and node representation learning, outperforming many competitive baselines in both tasks. We show that the framework of vGraph is quite flexible and can be easily extended to detect hierarchical communities.

将community deteciton 和node representation learning合为一个问题

each node can be represented by a mixture of communities, and each community is defined as a multinomial distribution over nodes.

结合邻居一代生成上下文信息

  • 4.Knowledge Graph Enhanced Community Detection and Characterization (WSDM 2019 B类)
    • Shreyansh Bhatt, Swati Padhee, Amit Sheth, Keke Chen ,Valerie Shalin, Derek Doran, and Brandon Minnery
    • [Paper]
    • [Java Reference]

Recent studies show that by combining network topology and node attributes, we can better understand community structures in complex networks. However, existing algorithms do not explore “contextually” similar node attribute values, and therefore may miss communities defined with abstract concepts. We propose a community detection and characterization algorithm that incorporates the contextual information of node attributes described by multiple domain-specific hierarchical concept graphs. The core problem is to find the context that can best summarize the nodes in communities, while also discovering communities aligned with the context summarizing communities. We formulate the two intertwined problems, optimal community-context computation, and community discovery, with a coordinate-ascent based algorithm that iteratively updates the nodes’ community label assignment with a community-context and computes the best context summarizing nodes of each community. Our unique contributions include (1) a composite metric on Informativeness and Purity criteria in searching for the best context summarizing nodes of a community; (2) a node similarity measure that incorporates the context-level similarity on multiple node attributes; and (3) an integrated algorithm that drives community structure discovery by appropriately weighing edges. Experimental results on public datasets show nearly 20 percent improvement on F-measure and Jaccard for discovering underlying community structure over the current state-of-the-art of community detection methods. Community structure characterization was also accurate to find appropriate community types for four datasets.

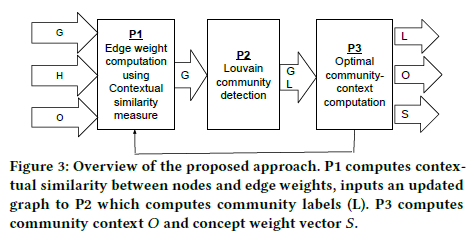
image

  • 5.Constrained Local Graph Clustering by Colored Random Walk (WWW 2019 A类)

Detecting local graph clusters is an important problem in big graph analysis. Given seed nodes in a graph, local clustering aims at finding subgraphs around the seed nodes, which consist of nodes highly relevant to the seed nodes. However, existing local clustering methods either allow only a single seed node, or assume all seed nodes are from the same cluster, which is not true in many real applications. Moreover, the assumption that all seed nodes are in a single cluster fails to use the crucial information of relations between seed nodes. In this paper, we propose a method to take advantage of such relationship. With prior knowledge of the community membership of the seed nodes, the method labels seed nodes in the same (different) community by the same (different) color. To further use this information, we introduce a color-based random walk mechanism, where colors are propagated from the seed nodes to every node in the graph. By the interaction of identical and distinct colors, we can enclose the supervision of seed nodes into the random walk process. We also propose a heuristic strategy to speed up the algorithm by more than 2 orders of magnitude. Experimental evaluations reveal that our clustering method outperforms state-of-the-art approaches by a large margin.

Community structure is ubiquitous in real-world complex networks. The task of community detection over these networks is of paramount importance in a variety of applications. Recently, nonnegative matrix factorization (NMF) has been widely adopted for community detection due to its great interpretability and its natural fitness for capturing the community membership of nodes. However, the existing NMF-based community detection approaches are shallow methods. They learn the community assignment by mapping the original network to the community membership space directly. Considering the complicated and diversified topology structures of real-world networks, it is highly possible that the mapping between the original network and the community membership space contains rather complex hierarchical information, which cannot be interpreted by classic shallow NMF-based approaches. Inspired by the unique feature representation learning capability of deep autoencoder, we propose a novel model, named Deep Autoencoder-like NMF (DANMF), for community detection. Similar to deep autoencoder, DANMF consists of an encoder component and a decoder component. This architecture empowers DANMF to learn the hierarchical mappings between the original network and the final community assignment with implicit low-to-high level hidden attributes of the original network learnt in the intermediate layers. Thus, DANMF should be better suited to the community detection task. Extensive experiments on benchmark datasets demonstrate that DANMF can achieve better performance than the state-of-the-art NMF-based community detection approaches.

  • 7.Adaptive Community Detection Incorporating Topology and Content in Social Networks (Knowledge-Based Systems 2018 二区)

In social network analysis, community detection is a basic step to understand the structure and function of networks. Some conventional community detection methods may have limited performance because they merely focus on the networks’ topological structure. Besides topology, content information is another significant aspect of social networks. Although some state-of-the-art methods started to combine these two aspects of information for the sake of the improvement of community partitioning, they often assume that topology and content carry similar information. In fact, for some examples of social networks, the hidden characteristics of content may unexpectedly mismatch with topology. To better cope with such situations, we introduce a novel community detection method under the framework of non-negative matrix factorization (NMF). Our proposed method integrates topology as well as content of networks and has an adaptive parameter (with two variations) to effectively control the contribution of content with respect to the identified mismatch degree. Based on the disjoint community partition result, we also introduce an additional overlapping community discovery algorithm, so that our new method can meet the application requirements of both disjoint and overlapping community detection. The case study using real social networks shows that our new method can simultaneously obtain the community structures and their corresponding semantic description, which is helpful to understand the semantics of communities. Related performance evaluations on both artificial and real networks further indicate that our method outperforms some state-of-the-art methods while exhibiting more robust behavior when the mismatch between topology and content is observed.

  • 8.Bayesian Robust Attributed Graph Clustering: Joint Learning of Partial Anomalies and Group Structure (AAAI 2018 A类)

We study the problem of robust attributed graph clustering. In real data, the clustering structure is often obfuscated due to anomalies or corruptions. While robust methods have been recently introduced that handle anomalies as part of the clustering process, they all fail to account for one core aspect: Since attributed graphs consist of two views (network structure and attributes) anomalies might materialize only partially, i.e. instances might be corrupted in one view but perfectly fit in the other. In this case, we can still derive meaningful cluster assignments. Existing works only consider complete anomalies. In this paper, we present a novel probabilistic generative model (PAICAN) that explicitly models partial anomalies by generalizing ideas of Degree Corrected Stochastic Block Models and Bernoulli Mixture Models. We provide a highly scalable variational inference approach with runtime complexity linear in the number of edges. The robustness of our model w.r.t. anomalies is demonstrated by our experimental study, outperforming state-of-the-art competitors.

  • 9.Discovering Fuzzy Structural Patterns for Graph Analytics (IEEE TFS 2018 一区)

Many real-world datasets can be represented as attributed graphs that contain vertices, each of which is associated with a set of attribute values. Discovering clusters, or communities, which are structural patterns in these graphs, are one of the most important tasks in graph analysis. To perform the task, a number of algorithms have been proposed. Some of them detect clusters of particular topological properties, whereas some others discover them mainly based on attribute information. Also, most of the algorithms discover disjoint clusters only. As a result, they may not be able to detect more meaningful clusters hidden in the attributed graph. To do so more effectively, we propose an algorithm, called FSPGA, to discover fuzzy structural patterns for graph analytics. FSPGA performs the task of cluster discovery as a fuzzy-constrained optimization problem, which takes into consideration both the graph topology and attribute values. FSPGA has been tested with both synthetic and real-world graph datasets and is found to be efficient and effective at detecting clusters in attributed graphs. FSPGA is a promising fuzzy algorithm for structural pattern detection in attributed graphs.

  • 10.Semi-Supervised Community Detection Using Structure and Size (ICDM 2018 B类)
  • 11.Ego-splitting Framework: from Non-Overlapping to Overlapping Clusters (KDD 2017 A类)
  • 12.[PDF]Graph Learning for Multiview Clustering (IEEE Transactions on Cybernetics 2017 一区)

Most existing graph-based clustering methods need a predefined graph and their clustering performance highly depends on the quality of the graph. Aiming to improve the multiview clustering performance, a graph learning-based method is proposed to improve the quality of the graph. Initial graphs are learned from data points of different views, and the initial graphs are further optimized with a rank constraint on the Laplacian matrix. Then, these optimized graphs are integrated into a global graph with a well-designed optimization procedure. The global graph is learned by the optimization procedure with the same rank constraint on its Laplacian matrix. Because of the rank constraint, the cluster indicators are obtained directly by the global graph without performing any graph cut technique and the k-means clustering. Experiments are conducted on several benchmark datasets to verify the effectiveness and superiority of the proposed graph learning-based multiview clustering algorithm comparing to the state-of-the-art methods.

Network embedding, aiming to learn the low-dimensional representations of nodes in networks, is of paramount importance in many real applications. One basic requirement of network embedding is to preserve the structure and inherent properties of the networks. While previous network embedding methods primarily preserve the microscopic structure, such as the first- and second-order proximities of nodes, the mesoscopic community structure, which is one of the most prominent feature of networks, is largely ignored. In this paper, we propose a novel Modularized Nonnegative Matrix Factorization (M-NMF) model to incorporate the community structure into network embedding. We exploit the consensus relationship between the representations of nodes and community structure, and then jointly optimize NMF based representation learning model and modularity based community detection model in a unified framework, which enables the learned representations of nodes to preserve both of the microscopic and community structures. We also provide efficient updating rules to infer the parameters of our model, together with the correctness and convergence guarantees. Extensive experimental results on a variety of real-world networks show the superior performance of the proposed method over the state-of-the-arts.

  • 14.Semi-supervised Clustering in Attributed Heterogeneous Information Networks (WWW 17 A类)

A heterogeneous information network (HIN) is one whose nodes model objects of different types and whose links model objects’ relationships. In many applications, such as social networks and RDF-based knowledge bases, information can be modeled as HINs. To enrich its information content, objects (as represented by nodes) in an HIN are typically associated with additional attributes. We call such an HIN an Attributed HIN or AHIN. We study the problem of clustering objects in an AHIN, taking into account objects’ similarities with respect to both object attribute values and their structural connectedness in the network. We show how supervision signal, expressed in the form of a must-link set and a cannot-link set, can be leveraged to improve clustering results. We put forward the SCHAIN algorithm to solve the clustering problem. We conduct extensive experiments comparing SCHAIN with other state-of-the-art clustering algorithms and show that SCHAIN outperforms the others in clustering quality.

  • 15.Learning Community Embedding with Community Detection and Node Embedding on Graph (CIKM 2017 B类)

In this paper, we study an important yet largely under-explored setting of graph embedding, i.e., embedding communities instead of each individual nodes. We find that community embedding is not only useful for community-level applications such as graph visualization, but also beneficial to both community detection and node classification. To learn such embedding, our insight hinges upon a closed loop among community embedding, community detection and node embedding. On the one hand, node embedding can help improve community detection, which outputs good communities for fitting better community embedding. On the other hand, community embedding can be used to optimize the node embedding by introducing a community-aware high-order proximity. Guided by this insight, we propose a novel community embedding framework that jointly solves the three tasks together. We evaluate such a framework on multiple real-world datasets, and show that it improves graph visualization and outperforms state-of-the-art baselines in various application tasks, e.g., community detection and node classification.

  • 16.MGAE: Marginalized Graph Autoencoder for Graph Clustering (CIKM 2017 B类)

Graph clustering aims to discovercommunity structures in networks, the task being fundamentally challenging mainly because the topology structure and the content of the graphs are difficult to represent for clustering analysis. Recently, graph clustering has moved from traditional shallow methods to deep learning approaches, thanks to the unique feature representation learning capability of deep learning. However, existing deep approaches for graph clustering can only exploit the structure information, while ignoring the content information associated with the nodes in a graph. In this paper, we propose a novel marginalized graph autoencoder (MGAE) algorithm for graph clustering. The key innovation of MGAE is that it advances the autoencoder to the graph domain, so graph representation learning can be carried out not only in a purely unsupervised setting by leveraging structure and content information, it can also be stacked in a deep fashion to learn effective representation. From a technical viewpoint, we propose a marginalized graph convolutional network to corrupt network node content, allowing node content to interact with network features, and marginalizes the corrupted features in a graph autoencoder context to learn graph feature representations. The learned features are fed into the spectral clustering algorithm for graph clustering. Experimental results on benchmark datasets demonstrate the superior performance of MGAE, compared to numerous baselines.

  • 17.Limited Random Walk Algorithm for Big Graph Data Clustering (Journal of Big Data 2016 一区)

Graph clustering is an important technique to understand the relationships between the vertices in a big graph. In this paper, we propose a novel random-walk-based graph clustering method. The proposed method restricts the reach of the walking agent using an inflation function and a normalization function. We analyze the behavior of the limited random walk procedure and propose a novel algorithm for both global and local graph clustering problems. Previous random-walk-based algorithms depend on the chosen fitness function to find the clusters around a seed vertex. The proposed algorithm tackles the problem in an entirely different manner. We use the limited random walk procedure to find attracting vertices in a graph and use them as features to cluster the vertices. According to the experimental results on the simulated graph data and the real-world big graph data, the proposed method is superior to the state-of-the-art methods in solving graph clustering problems. Since the proposed method uses the embarrassingly parallel paradigm, it can be efficiently implemented and embedded in any parallel computing environment such as a MapReduce framework. Given enough computing resources, we are capable of clustering graphs with millions of vertices and hundreds millions of edges in a reasonable time.

  • 18.Community Detection Based on Distance Dynamics (KDD 2015 A类)
In this paper, we introduce a new community detection algorithm, called Attractor, which automatically spots communities in a network by examining the changes of “distances” among nodes (i.e. distance dynamics). The fundamental idea is to envision the target network as an adaptive dynamical system, where each node interacts with its neighbors. The interaction will change the distances among nodes, while the distances will affect the interactions. Such interplay eventually leads to a steady distribution of distances, where the nodes sharing the same community move together and the nodes in different communities keep far away from each other. Building upon the distance dynamics, Attractor has several remarkable advantages: (a) It provides an intuitive way to analyze the community structure of a network, and more importantly, faithfully captures the natural communities (with high quality). (b) Attractor allows detecting communities on large-scale networks due to its low time complexity (O( E )). (c) Attractor is capable of discovering communities of arbitrary size, and thus small-size communities or anomalies, usually existing in real-world networks, can be well pinpointed. Extensive experiments show that our algorithm allows the effective and efficient community detection and has good performance compared to state-of-the-art algorithms.
  • 19.K-Clique Community Detection in Social NetworksBased on Formal Concept Analysis (IEEE Systems 2015 二区)

With the advent of ubiquitous sensing and networking, future social networks turn into cyber-physical interactions, which are attached with associated social attributes. Therefore, social network analysis is advancing the interconnections among cyber, physical, and social spaces. Community detection is an important issue in social network analysis. Users in a social network usually have some social interactions with their friends in a community because of their common interests or similar profiles. In this paper, an efficient algorithm of k-clique community detection using formal concept analysis (FCA) - a typical computational intelligence technique, namely, FCA-based k-clique community detection algorithm, is proposed. First, a formal context is constructed from a given social network by a modified adjacency matrix. Second, we define a type of special concept named k-equiconcept, which has the same k-size of extent and intent in a formal concept lattice. Then, we prove that the k-clique detection problem is equivalent to finding the k-equiconcepts. Finally, the efficient algorithms for detecting the k-cliques and k-clique communities are devised by virtue of k-equiconcepts and k-intent concepts, respectively. Experimental results demonstrate that the proposed algorithm has a higher F-measure value and significantly reduces the computational cost compared with previous works. In addition, a correlation between k and the number of k-clique communities is investigated.

-20.A Unified Semi-Supervised Community Detection Framework Using Latent Space Graph Regularization (IEEE TOC 2015 A类)

Community structure is one of the most important properties of complex networks and is a foundational concept in exploring and understanding networks. In real world, topology information alone is often inadequate to accurately find community structure due to its sparsity and noises. However, potential useful prior information can be obtained from domain knowledge in many applications. Thus, how to improve the community detection performance by combining network topology with prior information becomes an interesting and challenging problem. Previous efforts on utilizing such priors are either dedicated or insufficient. In this paper, we firstly present a unified interpretation to a group of existing community detection methods. And then based on this interpretation, we propose a unified semi-supervised framework to integrate network topology with prior information for community detection. If the prior information indicates that some nodes belong to the same community, we encode it by adding a graph regularization term to penalize the latent space dissimilarity of these nodes. This framework can be applied to many widely-used matrix-based community detection methods satisfying our interpretation, such as nonnegative matrix factorization, spectral clustering, and their variants. Extensive experiments on both synthetic and real networks show that the proposed framework significantly improves the accuracy of community detection, especially on networks with unclear structures.

  • 21.Community Detection Based on Structure and Content: A Content Propagation Perspective (ICDM 2015 B类)
  • 22.Nonnegative Matrix Tri-Factorization with Graph Regularization for Community Detection in Social Networks (IJCAI 2015 A类)

Community detection on social media is a classic and challenging task. In this paper, we study the problem of detecting communities by combining social relations and user generated content in social networks. We propose a nonnegative matrix tri-factorization (NMTF) based clustering framework with three types of graph regularization. The NMTF based clustering framework can combine the relations and content seamlessly and the graph regularization can capture user similarity, message similarity and user interaction explicitly. In order to design regularization components, we further exploit user similarity and message similarity in social networks. A unified optimization problem is proposed by integrating the NMTF framework and the graph regularization. Then we derive an iterative learning algorithm for this optimization problem. Extensive experiments are conducted on three real-world data sets and the experimental results demonstrate the effectiveness of the proposed method.

  • 23.Community Detection in Networks with Node Attributes (ICDM 2013 B类)
  • 24.A Model-based Approach to Attributed Graph Clustering (SIGMOID 2012 A类)

Graph clustering, also known as community detection, is a longstanding problem in data mining. However, with the proliferation of rich attribute information available for objects in real-world graphs, how to leverage structural and attribute information for clustering attributed graphs becomes a new challenge. Most existing works take a distance-based approach. They proposed various distance measures to combine structural and attribute information. In this paper, we consider an alternative view and propose a model-based approach to attributed graph clustering. We develop a Bayesian probabilistic model for attributed graphs. The model provides a principled and natural framework for capturing both structural and attribute aspects of a graph, while avoiding the artificial design of a distance measure. Clustering with the proposed model can be transformed into a probabilistic inference problem, for which we devise an efficient variational algorithm. Experimental results on large real-world datasets demonstrate that our method significantly outperforms the state-of-art distance-based attributed graph clustering method

  • 25.Graph Clustering Based on Structural/Attribute Similarities (WSDM 2009 B类)

Abstract

The goal of graph clustering is to partition vertices in a large graph into different clusters based on various criteria such as vertex connectivity or neighborhood similarity. Graph clustering techniques are very useful for detecting densely connected groups in a large graph. Many existing graph clustering methods mainly focus on the topological structure for clustering, but largely ignore the vertex properties which are often heterogenous. In this paper, we propose a novel graph clustering algorithm, SA-Cluster, based on both structural and attribute similarities through a unified distance measure. Our method partitions a large graph associated with attributes into k clusters so that each cluster contains a densely connected subgraph with homogeneous attribute values. An effective method is proposed to automatically learn the degree of contributions of structural similarity and attribute similarity. Theoretical analysis is provided to show that SA-Cluster is converging. Extensive experimental results demonstrate the effectiveness of SA-Cluster through comparison with the state-of-the-art graph clustering and summarization methods.

graph clustering measures vertex closeness based on connectivity (e.g., the number of possible paths between two vertices) and structural similarity (e.g., the number of common neighbors of two vertices);

while relational data clustering measures distance mainly based on attribute similarity (e.g.Euclidian distance between two attribute vectors).

image

The goal is to partition the graph into k clusters with cohesive intra-cluster structures and homogeneous attribute values. The problem is quite challenging because structural and attribute similarities are two seemingly independent, or even conflicting goals

  • 1.A Community Detection Algorithm Using Network Topologies and Rule-based Hierarchical Arc-merging Strategies (PLOS 2018)
  • 26.A Nonnegative Matrix Factorization Approach for Multiple Local Community Detection (ASONAM 2018)

Existing works on local community detection in social networks focus on finding one single community a few seed members are most likely to be in. In this work, we address a much harder problem of multiple local community detection and propose a Nonnegative Matrix Factorization algorithm for finding multiple local communities for a single seed chosen randomly in multiple ground truth communities. The number of detected communities for the seed is determined automatically by the algorithm. We first apply a Breadth-First Search to sample the input graph up to several levels depending on the network density. We then use Nonnegative Matrix Factorization on the adjacency matrix of the sampled subgraph to estimate the number of communities, and then cluster the nodes of the subgraph into communities. Our proposed method differs from the existing NMF-based community detection methods as it does not use “argmax” function to assign nodes to communities. Our method has been evaluated on real-world networks and shows good accuracy as evaluated by the F1 score when comparing with the state-of-the-art local community detection algorithm.

  • 12.Community Detection Using Preference Networks (Physica A 2018)

Community detection is the task of identifying clusters or groups of nodes in a network where nodes within the same group are more connected with each other than with nodes in different groups. It has practical uses in identifying similar functions or roles of nodes in many biological, social and computer networks. With the availability of very large networks in recent years, performance and scalability of community detection algorithms become crucial, i.e. if time complexity of an algorithm is high, it can not run on large networks. In this paper, we propose a new community detection algorithm, which has a local approach and is able to run on large networks. It has a simple and effective method; given a network, algorithm constructs a preference network of nodes where each node has a single outgoing edge showing its preferred node to be in the same community with. In such a preference network, each connected component is a community. Selection of the preferred node is performed using similarity based metrics of nodes. We use two alternatives for this purpose which can be calculated in 1-neighborhood of nodes, i.e. number of common neighbors of selector node and its neighbors and, the spread capability of neighbors around the selector node which is calculated by the gossip algorithm of Lind et.al. Our algorithm is tested on both computer generated LFR networks and real-life networks with ground-truth community structure. It can identify communities accurately in a fast way. It is local, scalable and suitable for distributed execution on large networks.

  • 25.Non-Linear Attributed Graph Clustering by Symmetric NMF with PU Learning (Arxiv 2018)

We consider the clustering problem of attributed graphs. Our challenge is how we can design an effective and efficient clustering method that precisely captures the hidden relationship between the topology and the attributes in real-world graphs. We propose Non-linear Attributed Graph Clustering by Symmetric Non-negative Matrix Factorization with Positive Unlabeled Learning. The features of our method are three holds. 1) it learns a non-linear projection function between the different cluster assignments of the topology and the attributes of graphs so as to capture the complicated relationship between the topology and the attributes in real-world graphs, 2) it leverages the positive unlabeled learning to take the effect of partially observed positive edges into the cluster assignment, and 3) it achieves efficient computational complexity, O((n2+mn)kt), where n is the vertex size, m is the attribute size, k is the number of clusters, and t is the number of iterations for learning the cluster assignment. We conducted experiments extensively for various clustering methods with various real datasets to validate that our method outperforms the former clustering methods regarding the clustering quality.

  • 41.Temporally Evolving Community Detection and Prediction in Content-Centric Networks (ECML 2018)

Abstract—In this work, we consider the problem of combining link, content and temporal analysis for community detection and prediction in evolving networks. Such temporal and content-rich networks occur in many real-life settings, such as bibliographic networks and question answering forums. Most of the work in the literature (that uses both content and structure) deals with static snapshots of networks, and they do not reflect the dynamic changes occurring over multiple snapshots. Incorporating dynamic changes in the communities into the analysis can also provide useful insights about the changes in the network such as the migration of authors across communities. In this work, we propose Chimera1 , a shared factorization model that can simultaneously account for graph links, content, and temporal analysis. This approach works by extracting the latent semantic structure of the network in multidimensional form, but in a way that takes into account the temporal continuity of these embeddings. Such an approach simplifies temporal analysis of the underlying network by using the embedding as a surrogate. A consequence of this simplification is that it is also possible to use this temporal sequence of embeddings to predict future communities. We present experimental results illustrating the effectiveness of the approach.

  • 13.Fluid Communities: A Community Detection Algorithm (CompleNet 2017)
    • Ferran Parés, Dario Garcia-Gasulla, Armand Vilalta, Jonatan Moreno, Eduard Ayguadé, Jesús Labarta, Ulises Cortés and Toyotaro Suzumura
    • [Paper]
    • [Python Reference]

We introduce a community detection algorithm (Fluid Communities) based on the idea of fluids interacting in an environment, expanding and contracting as a result of that interaction. Fluid Communities is based on the propagation methodology, which represents the state-of-the-art in terms of computational cost and scalability. While being highly efficient, Fluid Communities is able to find communities in synthetic graphs with an accuracy close to the current best alternatives. Additionally, Fluid Communities is the first propagation-based algorithm capable of identifying a variable number of communities in network. To illustrate the relevance of the algorithm, we evaluate the diversity of the communities found by Fluid Communities, and find them to be significantly different from the ones found by alternative methods.

  • 3.Fast Heuristic Algorithm for Multi-scale Hierarchical Community Detection (ASONAM 2017)
  • 30.[PDF]Subspace Based Network Community Detection Using Sparse Linear Coding (TKDE 2016 三区)

Information mining from networks by identifying communities is an important problem across a number of research fields including social science, biology, physics, and medicine. Most existing community detection algorithms are graph theoretic and lack the ability to detect accurate community boundaries if the ratio of intra-community to inter-community links is low. Also, algorithms based on modularity maximization may fail to resolve communities smaller than a specific size if the community size varies significantly. In this paper, we present a fundamentally different community detection algorithm based on the fact that each network community spans a different subspace in the geodesic space. Therefore, each node can only be efficiently represented as a linear combination of nodes spanning the same subspace. To make the process of community detection more robust, we use sparse linear coding with l 1 norm constraint. In order to find a community label for each node, sparse spectral clustering algorithm is used. The proposed community detection technique is compared with more than 10 state of the art methods on two benchmark networks (with known clusters) using normalized mutual information criterion. Our proposed algorithm outperformed existing algorithms with a significant margin on both benchmark networks. The proposed algorithm has also shown excellent performance on three real-world networks.

  • 6.ComSim: A Bipartite Community Detection Algorithm Using Cycle and Node’s Similarity (Complex Networks 2017)
  • 7.Evolutionary Graph Clustering for Protein Complex Identification(IEEE Transactions on Computational Biology and Bioinformatics 2016)

This paper presents a graph clustering algorithm, called EGCPI, to discover protein complexes in protein-protein interaction (PPI) networks. In performing its task, EGCPI takes into consideration both network topologies and attributes of interacting proteins, both of which have been shown to be important for protein complex discovery. EGCPI formulates the problem as an optimization problem and tackles it with evolutionary clustering. Given a PPI network, EGCPI first annotates each protein with corresponding attributes that are provided in Gene Ontology database. It then adopts a similarity measure to evaluate how similar the connected proteins are taking into consideration the network topology. Given this measure, EGCPI then discovers a number of graph clusters within which proteins are densely connected, based on an evolutionary strategy. At last, EGCPI identifies protein complexes in each discovered cluster based on the homogeneity of attributes performed by pairwise proteins. EGCPI has been tested with several real data sets and the experimental results show EGCPI is very effective on protein complex discovery, and the evolutionary clustering is helpful to identify protein complexes in PPI networks. The software of EGCPI can be downloaded via: https://github.com/ hetiantian1985/EGCPI.

  • 11.Modularity and Community Detection in Bipartite Networks (Phys. Rev. E 2007 三区)

The modularity of a network quantifies the extent, relative to a null model network, to which vertices cluster into community groups. We define a null model appropriate for bipartite networks, and use it to define a bipartite modularity. The bipartite modularity is presented in terms of a modularity matrix B; some key properties of the eigenspectrum of B are identified and used to describe an algorithm for identifying modules in bipartite networks. The algorithm is based on the idea that the modules in the two parts of the network are dependent, with each part mutually being used to induce the vertices for the other part into the modules. We apply the algorithm to real-world network data, showing that the algorithm successfully identifies the modular structure of bipartite networks.

  • 16.CDLIB: a python library to extract, compare and evaluate communities from complex networks (Applied Network Science, 2019)

Community Discovery is among the most studied problems in complex network analysis. During the last decade, many algorithms have been proposed to address such task; however, only a few of them have been integrated into a common framework, making it hard to use and compare different solutions. To support developers, researchers and practitioners, in this paper we introduce a python library - namely CDLIB - designed to serve this need. The aim of CDLIB is to allow easy and standardized access to a wide variety of network clustering algorithms, to evaluate and compare the results they provide, and to visualize them. It notably provides the largest available collection of community detection implementations, with a total of 39 algorithms.

  • 23.Learning Latent Factors for Community Identification and Summarization (IEEE Access 2018)

Network communities, which are also known as network clusters, are typical latent structures in network data. Vertices in each of these communities tend to interact more and share similar features with each other. Community identification and feature summarization are significant tasks of network analytics. To perform either of the two tasks, there have been several approaches proposed, taking into the consideration of different categories of information carried by the network, e.g., edge structure, node attributes, or both aforementioned. But few of them are able to discover communities and summarize their features simultaneously. To address this challenge, we propose a novel latent factor model for community identification and summarization (LFCIS). To perform the task, the LFCIS first formulates an objective function that evaluating the overall clustering quality taking into the consideration of both edge topology and node features in the network. In the objective function, the LFCIS also adopts an effective component that ensures those vertices sharing with both similar local structures and features to be located into the same clusters. To identify the optimal cluster membership for each vertex, a convergent algorithm for updating the variables in the objective function is derived and used by LFCIS. The LFCIS has been tested with six sets of network data, including synthetic and real networks, and compared with several state-of-the-art approaches. The experimental results show that the LFCIS outperforms most of the prevalent approaches to community discovery in social networks, and the LFCIS is able to identify the latent features that may characterize those discovered communities.

  • 33.Community Detection for Clustered Attributed Graphs via a Variational EM Algorithm (Big Data 2014)
  • 8.Intra-Graph Clustering Using Collaborative Similarity Measure (DPCD 2015)

Graph is an extremely versatile data structure in terms of its expressiveness and flexibility to model a range of real life phenomenon. Various networks like social networks, sensor networks and computer networks are represented and stored in the form of graphs. The analysis of these kind of graphs has an immense importance from quite a long time. It is performed from various aspects to get maximum out of such multifaceted information repository. When the analysis is targeted towards finding groups of vertices based on their similarity in a graph, clustering is the most conspicuous option. Previous graph clustering approaches either focus on the topological structure or attributes likeness, however, few recent methods constitutes both aspects simultaneously. Due to enormous computation requirements for similarity estimation, these methods are often suffered from scalability issues. In order to overcome this limitation, we introduce collaborative similarity measure (CSM) for intra-graph clustering. CSM is based on shortest path strategy, instead of all paths, to define structural and semantic relevance among vertices. First, we calculate the pair-wise similarity among vertices using CSM. Second, vertices are grouped together based on calculated similarity under k-Medoid framework. Empirical analysis, based on density, and entropy, proves the efficacy of CSM over existing measures. Moreover, CSM becomes a potential candidate for medium scaled graph analysis due to an order of magnitude less computations.

  • 15.[PDF]Detecting Community Structure Using Label Propagation with Weighted Coherent Neighborhood Propinquity (Physica A 2013)

Community detection has become an important methodology to understand the organization and function of various real-world networks. The label propagation algorithm (LPA) is an almost linear time algorithm proved to be effective in finding a good community structure. However, LPA has a limitation caused by its one-hop horizon. Specifically, each node in LPA adopts the label shared by most of its one-hop neighbors; much network topology information is lost in this process, which we believe is one of the main reasons for its instability and poor performance. Therefore in this paper we introduce a measure named weighted coherent neighborhood propinquity (weighted-CNP) to represent the probability that a pair of vertices are involved in the same community. In label update, a node adopts the label that has the maximum weighted-CNP instead of the one that is shared by most of its neighbors. We propose a dynamic and adaptive weighted-CNP called entropic-CNP by using the principal of entropy to modulate the weights. Furthermore, we propose a framework to integrate the weighted-CNP in other algorithms in detecting community structure. We test our algorithm on both computer-generated networks and real-world networks. The experimental results show that our algorithm is more robust and effective than LPA in large-scale networks.

  • 40.Graph Clustering with Dynamic Embedding (Arxiv 2017)

Graph clustering (or community detection) has long drawn enormous attention from the research on web mining and information networks. Recent literature on this topic has reached a consensus that node contents and link structures should be integrated for reliable graph clustering, especially in an unsupervised setting. However, existing methods based on shallow models often suffer from content noise and sparsity. In this work, we propose to utilize deep embedding for graph clustering, motivated by the well-recognized power of neural networks in learning intrinsic content representations. Upon that, we capture the dynamic nature of networks through the principle of influence propagation and calculate the dynamic network embedding. Network clusters are then detected based on the stable state of such an embedding. Unlike most existing embedding methods that are task-agnostic, we simultaneously solve for the underlying node representations and the optimal clustering assignments in an end-to-end manner. To provide more insight, we theoretically analyze our interpretation of network clusters and find its underlying connections with two widely applied approaches for network modeling. Extensive experimental results on six real-world datasets including both social networks and citation networks demonstrate the superiority of our proposed model over the state-of-the-art.

CATALOG
    FEATURED TAGS
    test paper web 程序员的自我修养